
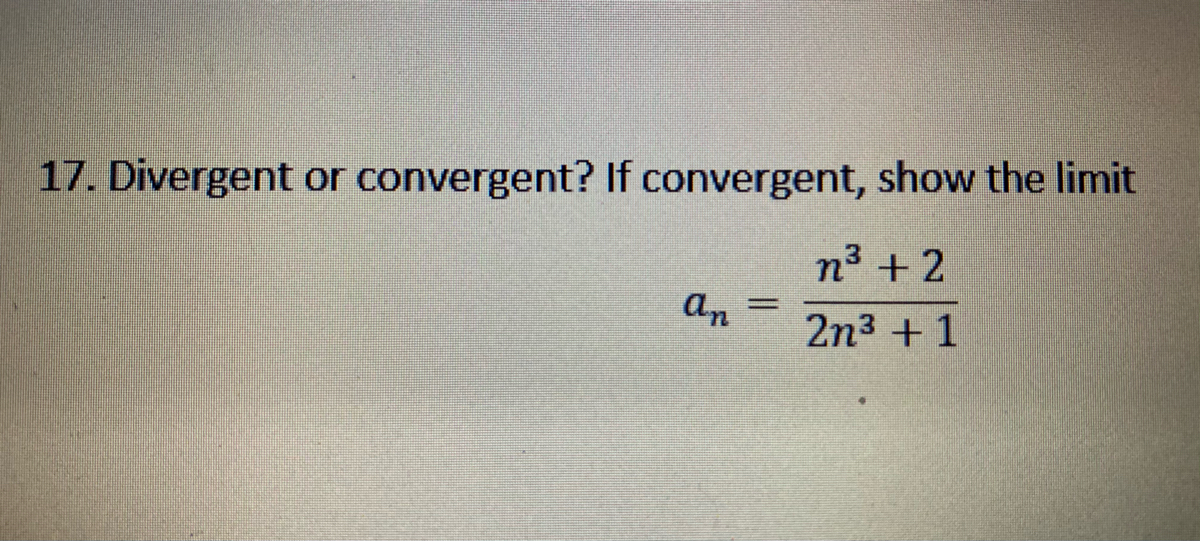
© Maplesoft, a division of Waterloo Maple Inc., 2023. Sample Problem The sequence an n diverges because as n approaches the terms an approach also. Sequences can diverge for different reasons. Just like a function, if a sequence doesn't converge, we say it diverges.
.jpg)
#Sequences convergence to divergence series
This will imply that the series cos n n + cos n is divergent. As n gets bigger and we move to the right on the graph, the dots get closer and closer to height 1.
#Sequences convergence to divergence how to
See how to use comparison tests to determine if a series is convergent or divergent with examples. The alternating series &Sigma − 1 n a n, with a n > 0, converges (at least conditionally) if a n is a monotonically decreasing sequence whose limit is zero. cos n n + cos n cos n n 1 1 + cos n n cos n n ( 1 cos n n + cos 2 n n + O ( 1 n 3 / 2)) cos n n + cos ( 2 n) 2 n 1 2 n + O ( 1 n 3 / 2) Now we are going to prove that the series cos n n and cos ( 2 n) 2 n are convergent using the Abel transform. Learn the convergence and divergence tests for an infinite series. We show how to find limits of sequences that converge, often by using the properties of limits for functions discussed earlier. In this section, we introduce sequences and define what it means for a sequence to converge or diverge. One reason sequences are so useful is that humans often times have a discrete way of thinking. Determine the convergence or divergence of a given sequence. Sequences allow us to take limits of discrete processes rather than those occuring over continuous time. ∑ n = n 0 a n converges or diverges accordingly as does ∫ k ∞ f x dx BASICS OF SEQUENCE CONVERGENCE AND DIVERGENCE IAN MILLER 0.1. If lim n → ∞ a n ≠ 0, then &Sigma a n diverges.į is a continuous on n 0, ∞, positive, decreasing function on k, ∞, for some k ≥ n 0 $\sum\limits_$?Īnd all the usual things you know for functions apply (except things like L'Hopital's Rule, which requires functions to be differentiable, which sequences are not).Table 8.3.1 details several tests for the convergence (or divergence) of infinite series. So in the same light to determine if a series is convergent like We have tried a couple different tests but all the info for limit/ratio test are for series. This is not homework I really need this explained and want to try to figure out why for my exam.ĭetermine whether the sequence converges or diverges and if it converges determine what it converges to. The Sequence Convergence Calculator is an online calculator used to determine whether a function is convergent or divergent by taking the limit of the. A series is said to divergent, it it does not. If the limit is larger than one, or infinite, then the series diverges. I will give you a problem from our study guide. A series is said to be convergent, if it converges to a value as the terms of series tends to infinity. If the limit of an(1/n) is less than one, then the series (absolutely) converges. If the series is an alternating series, determine whether it converges absolutely, converges conditionally, or diverges. Then determine if the series converges or diverges.
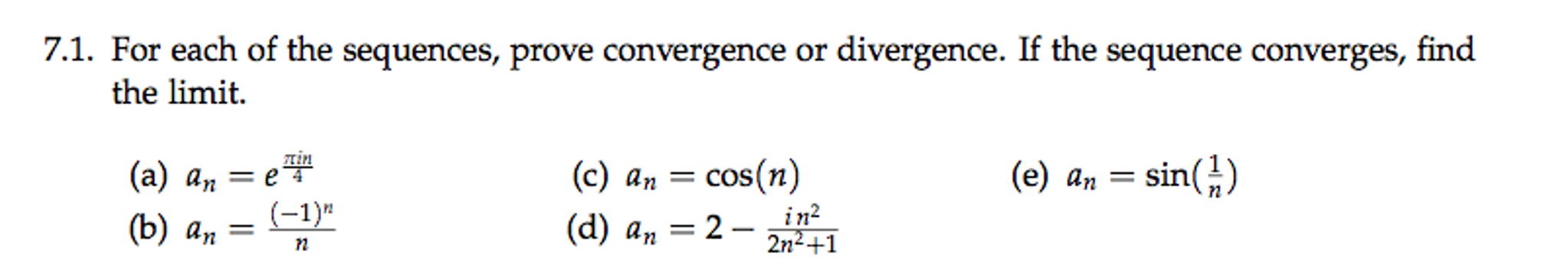
How do you solve such a problem for a sequence. For each of the following series, determine which convergence test is the best to use and explain why. On my professors study guide he gives us series and sequences and asks us to figure out if they converge/diverge. This is not necessary in order to do well. I understand the difference between the two but in all the book examples or online examples to discover if a series converges you are given a series. Here Im going to try to describe how to intuitively think about whether or not a series converges. I am studying for a Calc II exam and am confused by a fairly basic step with series and sequences.


 0 kommentar(er)
0 kommentar(er)
